Burnside引理和Polya定理

Veröffentlicht am 2016-02-16 | in 算法讲解

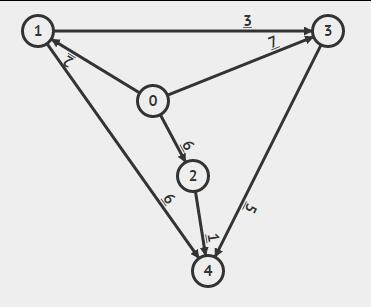
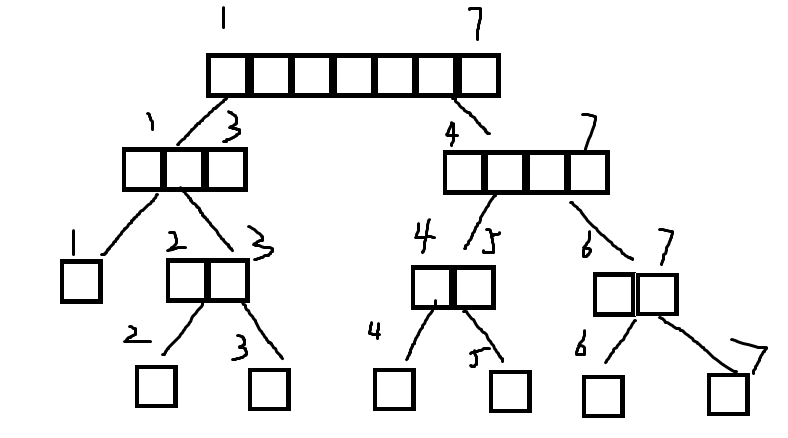
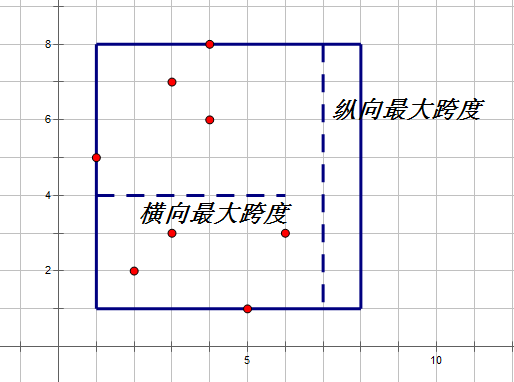
一些先修知识

群

群指的是一个集合$G$，连同一种运算$\cdot$，它结合集合中的任意两个元素$a,b$，记为$a\cdot b$。
群必须满足四个公理：

封闭性：$\forall a,b \in G,a \cdot b \in G$
结合性：$\forall a,b,c \in G,a \cdot b \cdot c = a \cdot (b \cdot c)$
单位元：$\exists e \in G,\forall a \in G, a \cdot e = a$
逆元：$\forall a,b \in G,\exists b,a \cdot b = e$

比如自然数和加法就是一个群，因为无论两个自然数怎么相加，结果依然是自然数，但是自然数和减法就不构成一个群，显然，整数和减法才构成一个群。

最短路算法

Veröffentlicht am 2016-02-12 | in 算法讲解

单源最短路

单源最短路的意思就是一个起点，算出到其他点的最短路，这里介绍三种算法，bellman-ford，spfa和dijkstra

BF算法

算法思想

BF是bellman_ford的简称，算法的想法非常简单，进行$|V|-1$次操作，每次操作对所有的边松弛。
松弛可以形象的理解为更新值，比如有一条从$u$到$v$的边，如果$u$上的值加上边的长度小于$v$上的值，那么就更新$v$上的值。
为什么这样做是对的呢？我们可以回顾整个过程，第一次操作，我们一定能将起点出去的点中的某一个点更新为最小值（这个点以后不会被更新），关于这点可以用反证法证明，如果没有一个点是更新完毕的，那么从起点到这个点必然存在一条比起点到这个点的边更短的路径，与假设矛盾。故而每次我们至少能确定一个点，所以总共需要$|V|-1$次（起点不用更新）。
最开始的图，0是起点

积性函数与线性筛法

Veröffentlicht am 2016-01-25 | in 算法讲解

从筛素数算法谈起

埃氏筛法

怎么得到$[1,N]$的所有素数，在很早很早以前（古希腊？）就有了方法。
算法的思想是用当前得到的数去筛掉他的倍数，这样每次遍历到的未被筛掉的数一定是素数。

int prime[MAX_N],tot=0;
bool check[MAX_N];
void getPrime(){
	memset(check,0,sizeof(check));
	for(int i=2;i<MAX_N;i++){
		if(check[i])continue;
		prime[tot++]=i;
		for(int j=2*i;j<MAX_N;j+=i)
			check[j]=1;
	}
}

不难发现，算法的每次会遍历$i$的所有倍数，所以算法的复杂度是调和级数的和，即$O(nlogn)$

欧拉筛法

仔细想想埃氏筛法的过程，就会发现每个数都会被它的所有素因子筛一遍，这样的操作是没有意义的，于是我们考虑一种更高效的筛法，使得每个数只被最小的素因子筛。

int prime[MAX_N],tot=0;
bool check[MAX_N];
void Euler(){
	memset(check,0,sizeof(check));
	for(int i=2;i<MAX_N;i++){
		if(!check[i])prime[tot++]=i;
		for(int j=0;j<tot;j++){
			if(prime[j]*i>=MAX_N)break;
			check[prime[j]*i]=1;
			if(i%prime[j]==0)break;
		}
	}
}

上述的算法由于每个数只被其素数筛掉，所以复杂度是$O(n)$的，故而又叫做线性筛法。

积性函数

定义

对于定义域在正整数的算术函数$f(n)$，若$f(1)=1$，且$f(ab)=f(a)f(b)$，其中$a,b$互质，则称$f(n)$为积性函数，如果$a,b$不互质，则称$f(n)$为完全积性函数。

性质

由算术基本定理，$f(n)$的值只由其素数因子的和其幂决定。
若$f(n)$是积性函数，$g(n)$是积性函数，那么$h(n)=f(n)g(n)$是积性函数
若$f(n)$是积性函数，那么$\sum_d|nf(d)$是积性函数

计算

如何得到积性函数往往是我们想关心的，由于上述性质来看，我们只要能够计算出$n$的最小的质数$p$的幂$k$，那么$f(n)=f(p^k)f(n/p^k)$。
所以问题便是求解一个数的最小素因子和其幂。我们发现欧拉筛法符合我们的要求，每个数只会被最小的素因子给筛掉。
由于素因子的幂不能用上述方法计算，所以只有因地制宜地计算。