一些先修知识
群
群指的是一个集合$G$,连同一种运算$\cdot$,它结合集合中的任意两个元素$a,b$,记为$a\cdot b$。
群必须满足四个公理:
封闭性:$\forall a,b \in G,a \cdot b \in G$
结合性:$\forall a,b,c \in G,a \cdot b \cdot c = a \cdot (b \cdot c)$
单位元:$\exists e \in G,\forall a \in G, a \cdot e = a$
逆元:$\forall a,b \in G,\exists b,a \cdot b = e$
比如自然数和加法就是一个群,因为无论两个自然数怎么相加,结果依然是自然数,但是自然数和减法就不构成一个群,显然,整数和减法才构成一个群。
置换
形象的理解就是字面上的意思,换位置,这是一个双射的函数$f$,我们可以用矩阵的形式写出来:
$$\begin{pmatrix}
1 & 2 & 3 & 4 & 5\\
2 & 4 & 5 & 3 & 1
\end{pmatrix}$$
上面这个矩阵指的是,将1这个位置的东西换到2,将2换到4,将3换到5,将4换到3,将5换到1。
置换群
对于一个$n$排列的置换集合$G$,我们定义置换的一种乘法运算,$g \cdot f$,其中$f,g \in G$。这种乘法运算是指先按照$f$进行置换,再按照$g$进行置换。例如:
$$f=\begin{pmatrix}1 & 2 & 3 & 4\\ 3 & 2 & 4 & 1\end{pmatrix}\;g=\begin{pmatrix}1 & 2 & 3 & 4\\ 2 & 4 & 3 & 1\end{pmatrix}$$
$$g \cdot f = \begin{pmatrix}1 & 2 & 3 & 4\\ 3 & 4 & 1 & 2\end{pmatrix}$$
显然,这种运算时满足结合律的:$f \cdot g \cdot h=f \cdot (g \cdot h)$,但是一般不满足交换律
恒等置换指的是置换后不变的置换,很明显,自然排列就是恒等置换:
$$\iota = \begin{pmatrix}1 & 2 & \cdots & n\\ 1 & 2 & \cdots & n\end{pmatrix}$$
我们定义$f^{-1}\in G$指置换$f\in G$的逆,即进行这两种置换后,原排列不变。
现在我们构造了这么一个集合和运算,显然这满足了群的四个特征,所以我们称之为置换群。
着色
定义$X$为${1,2,\cdots,n}$集合,$G$是$X$上的置换群,$X$上的着色,指的是将$X$中的每个元素指定一种颜色,$C$是$X$上的着色方案集合。
我们记置换$f$和着色$c$同时作用的时候为$f*c$
Burnside引理
现在我们尝试计算考虑置换的情况下,不同的染色方案的个数。
不动点$C(f)$
令$C(f)$为,在置换$f$作用时,$C$中不变的染色方案的集合,即:
$$C(f)= \{c\in C,f*c=c \} $$
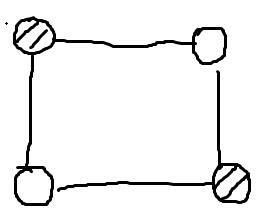
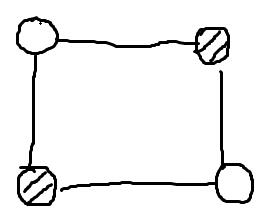
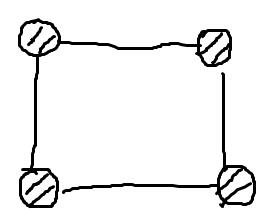
举个例子,我们现在有两种颜色,黑色和白色,去染正方形的四个角,那么在顺时针转180度的情况下,不变的染色数是4,如下图: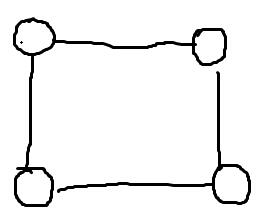
引理
引理指出,对于作用在$X$上的置换$G$和着色$C$来说,不同的方案数为所有置换的不动点的平均数。即:
$$N(G,C)=\frac{1}{|G|}\sum_{f\in G}|C(f)|$$
举个例子,我们要考察将正方形四个顶点染黑白色的不同方案数:
| 置换$f$ | 不动点$C(f)$大小 |
|---|---|
| 旋转0度 | 16 |
| 旋转90度 | 2 |
| 旋转180度 | 4 |
| 旋转270度 | 2 |
这样一来,不同的方案数就是:$N(G,C)=\frac{16+2+4+2}{4}=6$
证明
在证明之前,首先介绍一个概念:稳定核 $G(c)$,这是相对于不动点$C(f)$的概念。$G(c)$指的是染色$c$作用在$X$上时,$G$中使着色不变的置换的集合,即:
$$G(c)= \{ f\in G,f*c=c \} $$
我们首先计算有多少个着色和着色$c$是等价的,如果$f*c=g*c$,并且我们知道$g=f\cdot h$,我们想知道这个$h$是从哪里来的,由于着色和置换是满足结合律的,所以:
$$f*c=(f\cdot h)*c=f\cdot(h*c)$$
$$\therefore c=h*c$$
所以我们知道了,$h$是来自稳定核$G(c)$,换句话说,每个在$G$中的置换$f$,我们将$h \in G(c)$乘到这个置换上,会得到$|G(c)|$个置换,并且这些置换对于$c$是等价的,所以:
$$与c等价的个数=\frac{|G|}{|G(c)|}$$
整理一下思路,我们现在得到了两个重要的东西:
对于一个置换,有哪些着色不会改变,即$C(f)$
对于一个着色,有多少个着色和这个着色等价,即$\frac{|G|}{|G(c)|}$
现在我们尝试将两个概念联系起来,我们统计一下有多少对$(f,c)$,满足$f*c=c$。
首先我们从置换的角度来看,每个置换$f$都有$|C(f)|$个$(f,c)$,满足$f*c=c$,所以答案显然是:
$$\sum_{f\in G}|C(f)|$$
然后我们从着色的角度看,对于着色$c$来说,$f*c=c$中$f$的集合就是$G(c)$,由刚刚的推理我们知道$|G(c)|=\frac{|G|}{与c等价的个数}$,所以答案是:
$$\sum_{c\in C} \frac{|G|}{与c等价的个数}$$
如果我们对颜色进行分类,等价的颜色归为一类,那么每个等价类会对上面的和式贡献$|G|$的量,即总共贡献$N(G,C)*|G|$。
所以我们得到了Burnside引理:
$$N(G,C)=\frac{1}{|G|}\sum_{f\in G}|C(f)|$$
Polya定理
如果明白了Burnside引理,理解polya定理是很容易的。polya定理指出了如何计算不动点$C(f)$的大小。
对于一个置换来说,我们可以将其分解为若干个互不干扰的置换,比如置换:
$$f=\begin{pmatrix}1 & 2 & 3 & 4 & 5 & 6 & 7 & 8\\ 6 & 8 & 5 & 4 & 1 & 3 & 2 & 7\end{pmatrix}=[1\;6\;3\;5]\cdot[2\;8\;7]\cdot[4]$$
polya定理指出,对于一个置换$f$来说,其不动点的大小$|C(f)|$等于着色数的置换循环节的个数的幂,即:
$$|C(f)|=|C|^a$$
其中$a$表示循环节的个数,比如上面置换中,循环节的个数就是3。
证明
想必看到这里,脑袋都快炸了,所以我就不写规规矩矩的证明了。
我们来脑补一下,每个循环节很明显要涂成一个颜色,不然一置换,一定会有地方改变了颜色,所以,答案显然就是polya公式了。