代码：

代码戳我

Magic Spheres

题意：

给你三种颜色，每两个相同的颜色可以合成另外一种的一个颜色。问你能不能从初始的三种颜色，得到至少他给出的三种颜色的个数。

题解：

如果这题是恰好合成的话就是神题了，可如果是至少得话，就很简单了。如果一种颜色多了$x$个，那么他就能做出$x/2$这么多的贡献。现在统计一下有多少不足的，判断是否能用多余的补回去即可。

Sorting Railway Cars

题意：

给你一个排列，你要将他变成上升序列，每次只能将一个从中间提到开头，或者提到结尾。问你最少的操作次数。

题解：

考虑怎样才会操作最少，自然是不动的越多，则操作的次数最少。由于是个排列，所以当我们能够得到最长的上升自序列，并且这个子序列相邻的数的差是1，那么将不是这个子序列的数进行操作，就能得到最优解。
现在令$dp[i]$表示以数字$i$结尾的最长上升自然子序列。那么从左往右扫，$dp[a[i]]=dp[a[i]-1]+1$

Lazy Student

题意：

原来有一个图$G$，$G$的一个最小生成树$T$，现在告诉你每条边的权值，和其是否属于$T$，让你还原$G$。

题解：

很容易想到，为了方便处理，我们应当先将在$T$中的边排成一条链，然后来加入非树边。由于每次加入的时候，会构成一个环，我们需要保证每次加入的边都是这个环上最大的边。所以我们采取贪心的策略，首先将树边都从大到小排序，后将非树边从大到小插入，每次从链的左边开始连接。

Freelancer’s Dreams

题意：

给你一个矩阵$A_{2*n}$，求一个向量$T_{n*1}$，使得$A*T>=P$，其中$P$是个给出的$2*1$的向量，并且要使得$sum(T)$尽量小，并且$T(i)>=0$。

题解：

矩阵$A$其实是平面上的若干点。为了方便处理，我们加入三个点$(0,0),(0,ymax),(xmax,0)$，这样一定能找到一个凸壳，将这些点全部包括起来。
比如样例1的凸壳是这样的：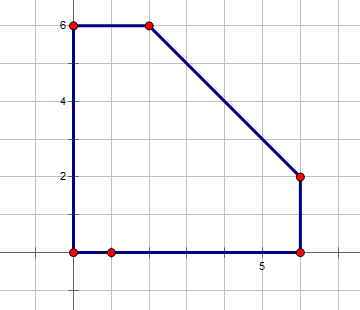

现在我们需要证明，在其中任意取若干点和$(0,0)$构成的向量进行线性组合，并且系数和$<=1$的情况下，得到的向量最多走到凸壳的边缘，而不能走出去。
当我们只取1个点的时候是必然的。
当我们取两个点的时候，显然，要让线性组合的向量尽量远，则必须取凸壳上相邻的向量，现在我们对其做线性组合：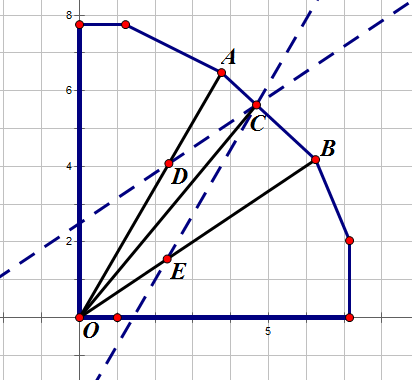

在上图中$C$是$AB$上一点，$CD//OB$，$CE//OA$，现在我们只需证明$\frac{OD}{OA}+\frac{OE}{OB}=1$，由相似三角形，这个结论是显然的。
当我们取三个及其以上的点的时候，由于平面上三个向量总是线性相关的，所以一定不如两个向量走得远。
综上，我们得出在这个凸壳内的向量无法在线性组合时，若系数和$<=1$，则必然超不出凸壳，且凸壳边缘时能到达的最远的地方。
有了上述的证明，我们知道，若我将凸壳整体扩大$t$倍，则相当于将系数和的范围控制在$sum(T)<=t$。那么我们现在只需要寻找最小的$t$，使得凸壳恰好包括点$P$即可。
由于具有二分性，所以我们可以二分$t$，至于怎么得到凸壳，怎么判断点时候在凸壳内，请自行Google