一个典型的路径统计问题

简单版的问题

从坐标系的$(0,0)$点出发到坐标系的$(n,n)$，每步只能向上或向右走一格，有多少种不同的方案数。
如下图是一个解：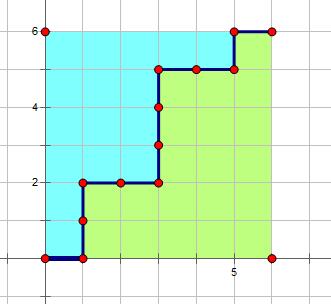

这个问题是十分简单的，很容易发现无论如何都要走$2n$步，并且其中$n$步是向上走的，其中$n$步是向左走的，那么总的方案数就是$\binom{2n}{n}$，即从$2n$个东西里面拿出来$n$个。

复杂一点

现在我们价格限制条件，路径不能越过中间的对角线，并且只能走下面的那个三角，如图所示：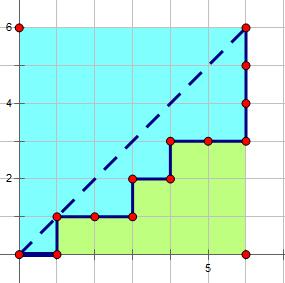

现在问题似乎变得不好求解了，但是我们依然可以从刚刚的角度出发。
忽略那个对角线，我们的方案是$\binom{2n}{n}$，现在我们只要减去超过对角线的就好。
如果路径超过了对角线，那么一定和$y=x+1$这条线相交：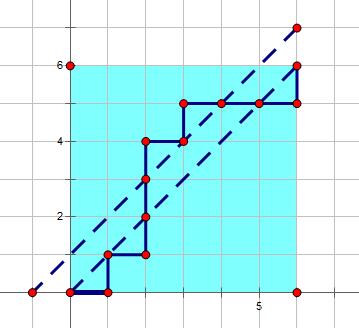

为了计算出这部分的方案数，我们将路径在第一次与$y=x+1$这条线相交之前的部分，沿着$y=x+1$对称过去：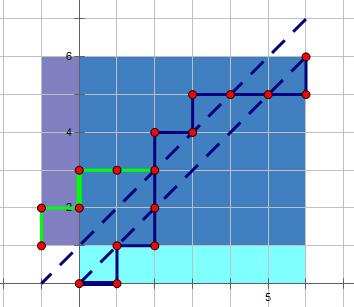

现在我们发现这部分的路径在对称后，都变成了从$(-1,1)$到$(n,n)$的路径，而且是单一映射，并且是满射，换句话说，每个超过了对角线的路径，都能找到从$(-1,1)$到$(n,n)$的路径与之对应，反之亦然。
所以我们就能得到方案数是
$$\binom{2n}{n}-\binom{2n}{n+1}$$
这就是卡特兰数，我们用$C_{n}$表示上面式子的值

卡特兰数的不同形态

封闭形式

首先是我们得到的，关于$n$的封闭形式：
$$C_{n}=\binom{2n}{n}-\binom{2n}{n+1},n>0$$
仔细推导得到下式
$$C_{n}=\frac{\binom{2n}{n}}{n+1},n>0$$

卷积形式

$$C_{n}=\sum_{k}C_kC_{n-1-k}+[n=0],n>0$$
这个式子的封闭形式就是上面的样子，我们可以去求母函数（或者z变换），然后再通过二项式定理得到证明，这里不多多赘述。

递推形式

这个形式是最有用的，因为这个形式允许我们在$O(nlogn)$的时间复杂度内求得第$n$项的值
$$C_0=1,C_{n+1}=\frac{2(2n+1)}{n+2}C_n$$

一些例子

括号序列

这是个常见的例子，我们现在有$n$个左括号，$n$个右括号，现在问有多少种排列，使得整个排列是个合法的括号序列：
()(())
我们从头到尾一个一个看括号，如果我们看到一个左括号，我们就向左走一步，否则就向上走一步，这问题就和不超过对角线的走法是一样的了。
所以答案就是$C_n$

凸多边形的三角剖分数

将$n+2$条边的凸多边形剖分成若干个三角形的不同方案数是多少，如下式$n=4$的方案数（图片来自wiki）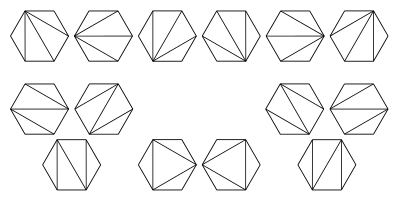

我们固定一条边，然后枚举与这条边构成三角形的点，然后我们就能将多边形分成三个部分——一个多边形，一个三角形，和一个多边形。
所以答案就是卡特兰数的卷积形式

两行人排队

现在有$2n$个人，每个人的身高从$1$到$2n$，现在排成两排，使得从左到右，从上到下都是递增的，如$n=5$有下面的一种排列方法：
1 3 4 5 6
2 7 8 9 10
这个问题本质上和括号序列是一样的，我们将左括号的下标写在第一行，右括号的下标写在第二行，就是答案。